A lvl H2 Maths: Differentiation

AJC Maths C Prelims 1997

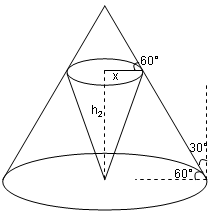
A circular hollow cone of height h cm and semi-vertical angle of 30° stands on horizontal ground. A smaller upright cone with base radius x cm just fits into the cone as shown.

(i) Show that the volume, V cm³ of the smaller cone is given by

$V = \frac{1}{3}\pi x^{2}\left(h - \sqrt{3} x \right)$

(ii) Prove that, as x varies, the maximum possible volume of the smaller cone is $\frac{4\pi }{243}h^{3}$ cm³

*************************

Answer:

(i) Let h₂ = height of smaller cone

(h - h₂) / x = tan 60°
h - h₂ = x√3
h₂ = h - x√3
Thus, volume of smaller cone
V = ⅓πx²h₂
$V = \frac{1}{3}\pi x^{2}\left(h - \sqrt{3} x \right)$ (shown)

(ii)
$V = \frac{1}{3} \pi x^{2}h - \frac{\sqrt{3}}{3}\pi x^{3}$
$\frac{dV}{dx} = \frac{2}{3}\pi xh - \sqrt{3}\pi x^{2} = 0$
$x = \frac{2}{2\sqrt{3}}h$ as x ≠ 0
$\frac{d^{2}V}{dx^{2}} = \frac{2}{3}\pi h - 2\pi x$

Substitute $x = \frac{2}{2\sqrt{3}}h$ into $\frac{d^{2}V}{dx^{2}} = \frac{2}{3}\pi h - 2\pi x$
$\frac{d^{2}V}{dx^{2}} = \frac{2\left(\sqrt{3} - 2 \right)}{3\sqrt{3}}\pi h$ and this is smaller than 0.

Hence, V is maximum when $x = \frac{2}{2\sqrt{3}}h$

Thus, maximum possible volume
$= \frac{1}{3}\pi \left(\frac{2}{3\sqrt{3}}h \right)^{2}\left(h - \sqrt{3}\left(\frac{2}{3\sqrt{3}}h \right) \right)$
$=\frac{4\pi }{243}h^{3}$ cm³ (proved)

Related Articles by Categories

A lvl H2 Maths%3A Differentiation