RGS P2 Prelim Q6b 1997
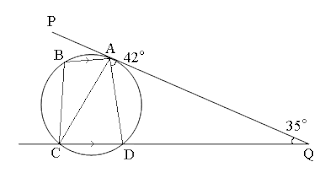
In the figure below, PAQ is the tangent at A to the circle ABCD and CDQ is a straight line. The lines BA and CD are parallel, angle DAQ = 42° and angle DQA = 35°. Calculate
(i) angle ACD
(ii) angle ABC
(iii) angle PAB
*************************
Answer:
(i) angle ACD = 42° (alternate angles for triangle in a circle)
(ii) angle ADC = 42° + 35° = 77° (Sum of external angles)
angle ABD = 180° - 77° = 103° (Opp angles of a cyclic quad adds up to 180°)
(iii) angle ADQ = 180° - 42° - 35°= 103° (angles in a triangle)
angle BAD = 103° (alternate angles)
angle PAB = 180° - 103° - 42° = 35° (angles on a straight line)